敏感词过滤应该是许多后端同事经常会遇到的需求,无论是评论、弹幕、文章,都需要做敏感词过滤处理来规避风险。在前端开发中,使用replace函数来替换字符串是我们的常规操作,在这之前我思考过如果用JavaScript来实现敏感词过滤该怎么做。在学习过程中,接触到了Trie树,瞬间有一种拨开云雾见青天的感觉。
所以,我这里算法使用的是AC(Aho–Corasick)自动机算法、设计模式使用单例模式。会简单的对方案进行阐述,主要是代码实现,需要注意的是,在这里将采用TypeScript编写。同时代码也上传至GitHub,点击此处查看本文完整代码
Aho–Corasick算法是由Alfred V. Aho和Margaret J.Corasick 发明的字符串搜索算法,用于在输入的一串字符串中匹配有限组“字典”中的子串。它与普通字符串匹配的不同点在于同时与所有字典串进行匹配。算法均摊情况下具有近似于线性的时间复杂度,约为字符串的长度加所有匹配的数量。
在正式进入到AC自动机算法之前,我们需要先了解Trie树。
Trie树(字典树)
在维基百科中,Trie 树的解释是这样的:
在计算机科学中,trie,又称前缀树或字典樹,是一种有序树,用于保存关联数组,其中的键通常是字符串。 与二叉查找树不同,键不是直接保存在节点中,而是由节点在树中的位置决定。 一个节点的所有子孙都有相同的前缀,也就是这个节点对应的字符串,而根节点对应空字符串。
构建Trie树
Trie树应用十分常见,例如搜索提示。如当输入一个网址,可以自动搜索出可能的选择。当没有完全匹配的搜索结果,可以返回前缀最相似的可能,当然我们这里不做过多的讨论。
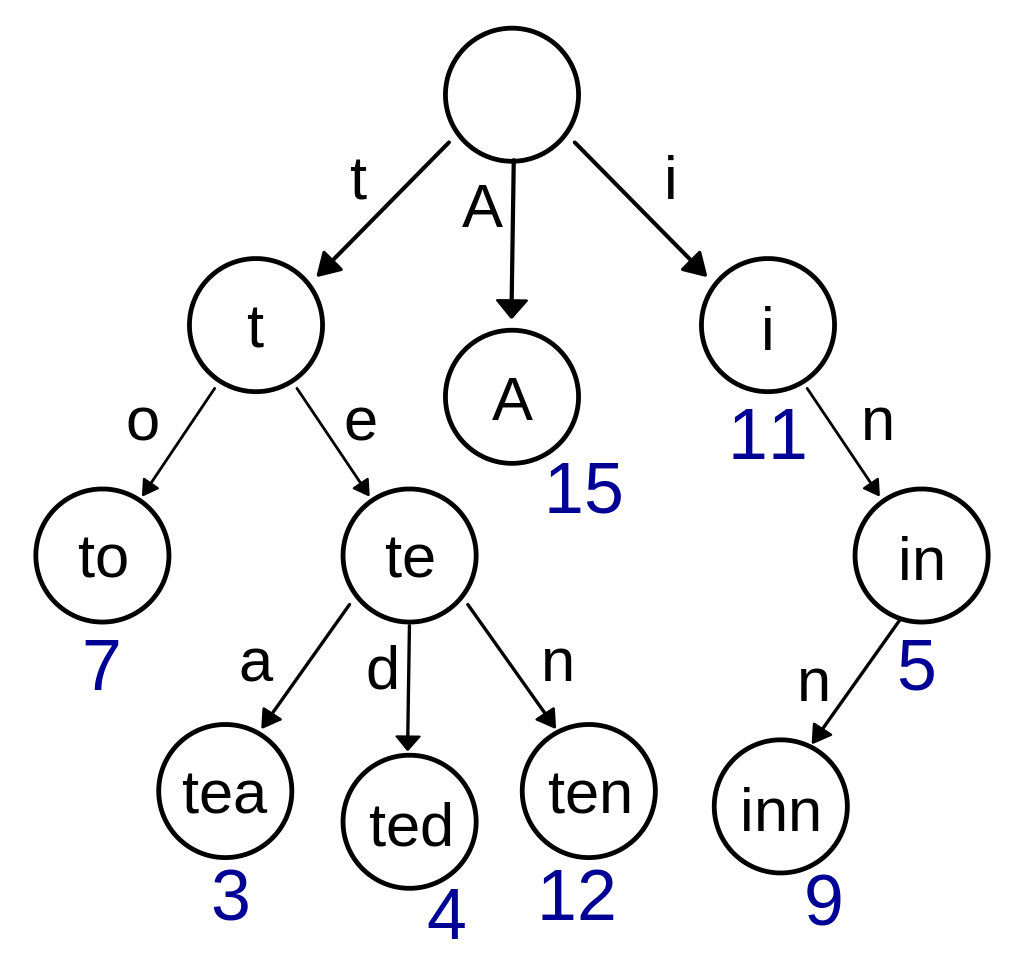
上图是一个保存了8个键的trie结构,“A”, “to”, “tea”, “ted”, “ten”, “i”, “in”, and “inn”。
但这种描述可能不太清晰,我们举一个例子:
有这么一个过滤规则,以下词组都要被过滤:['atd', 'aq', 'bs', 'bsc', 'qf'],需要被过滤的字符串是:acatdaabsc。那么首先我们需要构建一个Trie树,下图就是基于上述关键词构建的Trie树:

与我们熟悉的二叉树不同的是,这里的根节点ROOT没有包含任何数据,子节点也没有数量的限制,其每一个分支都代表着一个完整的字符串。
如果我们向上述过滤词中再加入一个“atp”,那么Trie树就会构建成这样:

那么我们也可以看到“atd”与“atp”拥有公共前缀“at”。当然,如果我们仔细看上面的过滤词组,会发现我们过滤了“bs”与“bsc”,那么他们的公共前缀就是bs,但与“atd”、“atp”不同的是,过滤词组中并没有“at”,那么这种情况我们应该怎么处理呢?
很简单,因为我们需要过滤掉“bs”,但不需要过滤“at”,那么我们就在“bs”的最后一个节点“s”处做一个标记,告诉程序分支到此处组成的单词是需要过滤的。当把所有的单词节点标记后,树会是这样的。

那么确定了Trie树是个什么样子,我们就可以用代码去实现了。首先我们从最基本的节点开始构建,从该图示可以看到,一个子节点包含了三个要素:
- 当前的值
- 该子节点的子节点
- 分支到此处是否是一个单词
那么我们就按照上述信息构建一个Node类,但此时这个Node类并不是我们最终需要的样子,在这里只是满足了构建一个Trie树的需求:
// 子节点的接口
interface Children {
[key: string]: Node
}
export default class Node {
// 节点值
public key: string
// 是否为单词最后节点(重要,后面详述)
public word: boolean
// 子节点的引用(重要,后面详述)
public children: Children = {}
constructor (key: string, word: boolean = false) {
this.key = key
this.word = word
}
}
在上面我们就已经知道了,Trie树根节点不保存数据,那么我们现在可以构建一个基础的Tree类,同时我们知道该类应该有一个插入和搜索方法,但此时我们不去实现这两个方法:
import Node from './node'
// 子节点的接口
interface Children {
[key: string]: Node
}
export default class Tree {
// 保存子节点的引用
public root: Node
constructor () {
this.root = new Node('root')
}
/**
* 插入数据
*/
insert () {}
/**
* 搜索节点
*/
search () {}
}
在之前的图中可以看到,在Trie树十分简单,通俗的说就是将一个关键词抽离成单字符,并构建出这个单字符的依赖顺序,重复这样的操作就构成了Trie树。
好了,上面我们已经构建了基本的Trie树,也明白了该怎样操作,那么我们就从insert方法开始吧:
export default class Tree {
// ...省略其他代码
/**
* 插入节点/第1层
*/
insert (key: string): boolean {
if (!key) return false
// 需要注意的是,插入的关键词key可能是单字符,也可能不是
// 将key打散成数组方便操作
let keyArr = key.split('')
// 获取key的第一个单字符
let firstKey = keyArr.shift()
// 获取root的子节点,this.root是Node的实例,所以children是一个对象
let children = this.root.children
let len = keyArr.length
// 这里是树第一层的处理
// 关键词第一个单字符在不在root的children里,不在的话我们就添加,这里之所以把第一个单字符提出来单独处理,是为了后续操作方便
if (!children[firstKey]) {
// 同时这里要判断剩余数组的长度,如果说传入的本身就是个单字符,就证明该单字符就是我们需要过滤的,我们需要给他打上word标记
children[firstKey] = len
? new Node(firstKey)
: new Node(firstKey, true)
} else if (!len) {
// 如果后续传入的是个单字符关键词(位于树第一层),我们需要打上word标记
firstNode.word = true
}
// 这里是树N+1曾的处理
// 其他多余的key使用insertNode递归写入树中
if (keyArr.length >= 1) {
this.insertNode(children[firstKey], keyArr)
}
return true
}
/**
* 插入节点/N+1层
* @param node
* @param word
*/
insertNode(node: Node, word: string[]) {
let len = word.length
// 因为是一个递归,这里的帝国条件是word长度 >= 0
if (len) {
let children: Children
children = node.children
const key = word.shift()
let item = children[key]
const isWord = len === 1
// 这里判断该节点有没有相应子节点
if (!item) {
// 没有即插入新的
item = new Node(key, isWord)
} else {
// 有则更新它的word标记
item.word = isWord
}
// 将结果重置到树的相应位置
children[key] = item
// 下一轮递归
this.insertNode(item, word)
}
}
// ...省略其他代码
}
至此,我们已经完整的构建了一棵Trie树的结构,并定义了insert方法,构建完成后,就需要查找,那么下面我们就去定义它的查找方法。
查找
既然我们知道也构建好了Trie树的结构,那么怎么去查找相关关键字并实现过滤呢?我们先定义这样一些数据备用:
- 过滤词组:
['atd', 'atp', 'aq', 'bs', 'bsc', 'gf'] - 过滤字符串:
acatdaabsc
我们将所有数据图形化:

同时,我们再定义三个索引/指针:
- startIndex:将保存匹配到的关键词起始位置索引/初始指向a
- endIndex:将保存匹配到的关键词结束位置索引/初始指向a
- treeIndex:将保存Trie树位置索引/初始指向ROOT
完成后,我们就来看看Trie树怎么实现查找的,
第一步:endIndex位置指向a时(这是初始值)
一开始,程序询问Trie树treeIndex指向的ROOT节点有没有a这个子节点,显然是有的。那么startIndex赋值为a位置的索引0(虽然一开始也是0,但这不重要)。同时改变treeIndex指向,让其指向a节点。判断此节点是否是一个完整的单词(即需要过滤关键词的最后一个字符),显然不是。
第二步:endIndex后移指向c时
endIndex后移一位指向c:

程序询问Trie树treeIndex指向的a节点有没有c这个子节点,显然是没有的。那么startIndex赋值为c位置的索引1。同时改变treeIndex指向,让其重新指向ROOT节点。
第三步:endIndex后移指向a时
endIndex后移一位指向a:

这里会完全重复第一步的操作,但是startIndex指向的时第二个a的索引2。
此时,startIndex = endIndex = 2,他们都指向了a,treeIndex又重新指向了树节点a。
第四步:endIndex后移指向t时
endIndex后移一位指向t:

程序询问Trie树treeIndex指向的a节点有没有t这个子节点,我们知道有,符合需求。startIndex位置不变,同时改变treeIndex指向,让其指向新找到的t节点。判断此节点是否是一个完整的单词。
第五步:endIndex后移指向d时
endIndex后移一位指向d:

程序询问Trie树treeIndex指向的t节点有没有d这个子节点,这里有d/p两个子节点,符合需求。startIndex位置不变,同时改变treeIndex指向,让其指向新找到的d节点。

判断此节点是否是一个完整的单词,很幸运,这次是一个完整待过滤关键词atd。至此,我们就找到了字符串中第一个关键词。
找到后,我们endIndex后移,并使startIndex = endIndex,treeIndex重新指向ROOT,开启新一轮的匹配。重复这个过程,就完成了查找。
那么在了解了上述查找过程之后,我们可以先完成一个基本查找,查找单个节点存不存在以做备用:
export default class Tree {
// ...省略其他代码
/**
* 搜索节点
* @param key
* @param node
*/
search(key: string, node: Children = this.root.children): Node | undefined {
// 这个搜索十分简单,只传入的子节点是否有相应的节点
return node[key]
}
// ...省略其他代码
}
Aho–Corasick算法(也称AC自动机/状态机)
寻找failure指针/索引
Trie树是AC算法的基础,AC算法有三个特别重要的概念,网上有很多文章,但搜索出来大多都是一样的,有些关键点没写明白,看着十分吃力。在这里,我会尝试去让这些概念性的东西具体化。
我们先把上面的Node类拿下来:
export default class Node {
// 节点值
public key: string
// 是否为单词最后节点(重要,后面详述)
public word: boolean
// 子节点的引用(重要,后面详述)
public children: Children = {}
constructor (key: string, word: boolean = false) {
this.key = key
this.word = word
}
}
那么AC算法的三个关键是什么呢?与Node类有什么关系呢?通俗的讲是这么三个状态(有的称之为函数,有的称之为表):
- success/output状态:表示节点到此处就已经构成了个完整的关键词(Node类的word标记)。
- goto状态:表示此节点构成的关键词还不完整,需要进入他的下一个子节点匹配(Node类的children)
- failure状态(也称失去匹配,下面简称【失配】状态):表示此节点构成的关键词还不完整,但==无法进入到下一个子节点==(在当前children里找不到了)。需要告诉程序,失配后怎么走。
在这之前,失配我们直接就返回到了ROOT,但AC算法不一样,它利用【failure状态/函数/表】指定程序在失配后的表现,不必每次失配都重新开始,这样能节省不少的时间。
好的,我们看到AC算法的两个状态Trie树都具备,只有failure状态是新加的,那么我们就着重讲一下failure状态,在这之前,我们重新构造一下Node类:
export default class Node {
// 节点值
public key: string
// 是否为单词最后节点
public word: boolean
// 子节点的引用
public children: Children = {}
// 父节点的引用
public parent: Node | undefined
// failure表,用于失配后的跳转
public failure: Node | undefined = undefined
constructor (key: string, parent: Node | undefined = undefined, word: boolean = false) {
this.key = key
this.parent = parent
this.word = word
}
}
可以看到,我这里新增了两个公共属性parent父节点及failure失配(失去匹配)后指向的节点。那么Node类的结构变化以后,Tree类的也需要相应的改变。
export default class Tree {
// ...省略其他代码
insert (key: string): boolean {
if (!key) return false
let keyArr = key.split('')
let firstKey = keyArr.shift()
let children = this.root.children
let len = keyArr.length
if (!children[firstKey]) {
// 变化处
children[firstKey] = len
? new Node(firstKey)
: new Node(firstKey, undefined, true)
} else if (!len) {
firstNode.word = true
}
if (keyArr.length >= 1) {
this.insertNode(children[firstKey], keyArr)
}
return true
}
insertNode(node: Node, word: string[]) {
let len = word.length
if (len) {
let children: Children
children = node.children
const key = word.shift()
let item = children[key]
const isWord = len === 1
if (!item) {
// 变化处
item = new Node(key, node, isWord)
} else {
item.word = isWord
}
children[key] = item
this.insertNode(item, word)
}
}
// ...省略其他代码
}
很简单,只有两个地方变化了,目的是实例化时传入parent属性。将两个基础类构造完成之后,我们就要详细说一说failure状态了,先看['HER', 'HEQ', 'SHR']构建的树:

==在下面的描述中,我将failure指针/索引,为便于叙述,我通俗的说成“failure指向”==
在这张图中,虚线表示failure后的指向,上面我们也说到failure状态的作用,就是在失配的时候告诉程序往哪里走,为什么要这么做,从这张表我们可以很清楚的看到,当我们匹配SHER时,程序会走右边的分支,当走到S > H > E时,会出现失配,怎么办?可能有小伙伴会想到回滚到ROOT从H开始重新匹配,但这样回溯是有成本的,我们既然走了H节点,为什么要回溯呢?
这个时候failure就发挥作用了,我们看到右分支的H有一条虚线指向了左分支的H,我们也知道这就是failure的指向,通过这个指向,我们很轻松的将当前状态移交过去。程序继续匹配E > R,加上移交过来的H,我们可以轻松的匹配到HER。
到了这里,我想小伙伴已经体会到了AC算法的美妙之处,那么就有人会问了,这个failure的指向怎么拿到呢?其实就是一句话:
问:假设有一个节点为currNode,它的子节点是childNode,那么子节点childNode的failure指向怎么求?
解:首先,我们需要找到childNode父节点currNode的failure指向,假设这个指向是Q的话,我们就要看看Q的孩子(children属性)中有没有与childNode字符相同(key相同)的节点,如果有的话,这个节点就是childNode的failure指向。如果没有,我们就需要沿着currNode -> failure -> failure重复上述过程,如果一直没找到,就将其指向root。
那么以上,就是寻找failure指向的思路,具体为什么这么做可以查阅相关资料。
需要注意的是,我们在构建Trie树时,并不知道failure指向到哪里的,所以failure指向需要在Trie树构建完成后插入。
那么我们再定义一个方法构建failure指向,但我们需要先看下面这幅图:

从图中可以看到,failure指向的构建是从上至下一层一层的完成的,第一层都是指向root:
export default class Tree {
// ...省略其他代码
/**
* 创建Failure表
*/
_createFailureTable() {
// 获取树第一层
let currQueue: Array<Node> = Object.values(this.root.children)
while (currQueue.length > 0) {
let nextQueue: Array<Node> = []
for (let i = 0; i < currQueue.length; i++) {
let node: Node = currQueue[i]
let key = node.key
let parent = node.parent
node.failure = this.root
// 获取树下一层
for (let k in node.children) {
nextQueue.push(node.children[k])
}
if (parent) {
let failure: any = parent.failure
while (failure) {
let children: any = failure.children[key]
// 判断是否到了根节点
if (children) {
node.failure = children
break
}
failure = failure.failure
}
}
}
currQueue = nextQueue
}
}
// ...省略其他代码
}
完成上面代码,我们就彻底完成了整个AC算法的前置准备工作也是核心部分。
字符串匹配
最后对字符串进行关键词匹配,思路不难但有点庞杂,是核心点,关键点在于获取failure指针的定位,当匹配成功后,获取整个字符串。但如何获取匹配成功的关键词,我看到有些方案是回溯分支,但我是觉得没必要,因为匹配成功,程序已经走了之前的分支,为什么还要再次回溯呢?下面我们直接再代码上看:
_filterFn(word: string, every: boolean = false, replace: boolean = true): FilterValue {
let startIndex = 0
let endIndex = startIndex
const wordLen = word.length
// 因为英文匹配我直接转换成了全大写,就需要保存一个原始文本
let originalWord: string = word
// 保存过滤的关键字
let filterKeywords: Array<string> = []
// 全部转换成大写
word = word.toLocaleUpperCase()
// 是否过滤文本
let isReplace = replace
let filterText: string = ''
// 是否通过,字符串无敏感词
let isPass = true
// 正在进行划词判断
let isJudge: boolean = false
let judgeText: string = ''
// 上一个Node与下一个Node
let prevNode: Node = this.root
let currNode: Node | boolean
for (endIndex; endIndex <= wordLen; endIndex++) {
let key: string = word[endIndex]
let originalKey: string = originalWord[endIndex]
// 查找当前Node
currNode = this.search(key, prevNode.children)
// 判断是否处于正在判断状态isJudge,且还能继续匹配(currNode为Node)
if (isJudge && currNode) { // ①
judgeText += originalKey
prevNode = currNode
continue
} else if (isJudge && prevNode.word) {
// 处于正在匹配状态,不能继续匹配,上一个Node有word标记,证明已经匹配成功了
// 这里用作快速查找方法every
isPass = false
if (every) break
// 原始字符串在这里做关键词替换,并保存被替换的关键词
if (isReplace) filterText += '*'.repeat(endIndex - startIndex)
filterKeywords.push(word.slice(startIndex, endIndex))
} else {
// 将①保存的临时文本重新添加到过滤文本中,因为可能最后状态是失配
filterText += judgeText
}
// 直接在分支上找不到,需要走failure,这里的查找也与构建failure时相似
if (!currNode) {
let failure: Node = prevNode.failure
while (failure) {
currNode = this.search(key, failure.children)
if (currNode) break
failure = failure.failure
}
}
if (currNode) {
judgeText = originalKey
isJudge = true
prevNode = currNode
} else {
judgeText = ''
isJudge = false
prevNode = this.root
if (isReplace && key !== undefined) filterText += originalKey
}
startIndex = endIndex
}
return {
text: isReplace ? filterText : originalWord,
filter: [...new Set(filterKeywords)],
pass: isPass
}
}
使用:
let m = new Mint(['淘宝', '拼多多', '京东'])
console.log(m.filterSync('双十一在淘宝买东西,618在京东买东西,当然你也可以在拼多多买东西。'))
/* {
text: '双十一在**买东西,618在**买东西,当然你也可以在***买东西。',
filter: [ '淘宝', '京东', '拼多多' ],
pass: false
} */
console.log(m.everySync('测试这条语句是否能通过')) // true
console.log(m.everySync('测试这条语句是否能通过,加上任意一个关键词京东')) // false
那么自此,整个流程就通了,当然这只是关键代码,具体代码我已上传至Github,当然,因本人能力及知识水平有限,难免有所错误,如若发现,欢迎大家指正。
单例模式
之所以使用单例模式,因为关键词构建成树是有空间成本的,我们没有必要在代码里使用多个实例,因为关键字完全可以放在一个文件里。
let instance: Mint | undefined = undefined
class Mint extends Tree {
// 是否替换原文本敏感词
constructor(keywords: Array<string>) {
if (instance) return instance
super()
if (!(keywords instanceof Array && keywords.length >= 1)) {
console.error('mint-filter:未将过滤词数组传入!')
return
}
// 创建Trie树
for (let item of keywords) {
if (!item) continue
this.insert(item.toLocaleUpperCase())
}
this._createFailureTable()
instance = this
}
// ...省略其他代码
}
性能
测试字符串包含随机生成的汉字、字母、数字。 以下测试均在20000个随机敏感词构建的树下进行测试,每组测试6次取平均值:
| 编号 | 字符串长度 | 不替换敏感词 | 替换敏感词 |
|---|---|---|---|
| 1 | 1000 | 0.987ms | 1.088ms |
| 2 | 5000 | 3.095ms | 3.252ms |
| 3 | 10000 | 9.133ms | 9.881ms |
| 4 | 20000 | 10.569ms | 12.032ms |
| 5 | 50000 | 15.741ms | 23.606ms |
| 6 | 100000 | 31.072ms | 46.681ms |
不觉明厉
